いまさらだが、世界のナベアツという芸人がいる。「3の倍数と、3がつく数字の時にアホになる」というネタをやっている芸人だ。
一見誰にでも出来そうな芸に思ってしまうが、該当する値で確実にリアクションを取るというのは高度な技術でありつつ、やっぱり練習すれば誰にでもできるんじゃねーの?と思ってしまう。でも「練習すれば誰にでもできる」ことに対して本当に練習をやっているのが凄いのである。
ウィキペディアで調べてみるとこのネタには様々なバリエーションが存在するらしいが、基本形は「3の倍数と、3がつく数字の時にアホになる」だ。
そこで思った。ナベアツはどこまでアホになるのだろう?ナベアツの芸が数字の40で終わったとしよう。1から40までの数を調べてみると。
- 3の倍数と、3がつく数字
- 3,6,9,12,13,15,18,21,23,24,27,30,31,32,33,34,35,36,37,38,39
- それ以外の数字
- 1,2,4,5,7,8,10,11,14,16,17,19,20,22,25,26,28,29,40
40個の数字のうち、21個がアホになる数値だ。つまりナベアツは52.5%アホだといえる。 これを突き詰めるとナベアツはいつまでもアホになるはずだ。だって3を使わない数ってのは「0,1,2,4,5,6,7,8,9」の9個の組み合わせ。ってことは3を使わない数が存在する割合は、0.9の桁数乗だ。つまり桁数が増えるたんびに3を使う数字の割合は増えていく。桁数が無限になれば割合が限りなく1に近づく。さらに3の倍数でもアホになるので1に近づく速度はもっと早い。つまりほぼ100%になるということだ。
無限になればナベアツが100%アホになることはわかった。無限を求めることはできないので、ナベアツが99.9%アホになる数を求めてみることにした。一体どこまで桁数を増やせば99.9%アホになるのか?というわけで「1から10のn乗までのうち、ナベアツがアホでいる自然数が存在する割合(nは2以上)」を計算できる式を作ってみた。それが以下の式だ。間違ってたらゴメン。
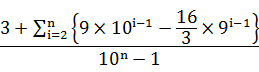
この式に100をかけるとパーセンテージになる。計算するとn=62の時に99.9%を超えている。つまり10の62乗までいくとナベアツは99.9%以上アホの状態ということだ。10の62乗とは百那由他のことで、実際に書くと10000000000000000000000000000000000000000000000000000000000000という数字だ。
しかしテレビで一度しか見たことがない芸人相手に、僕は一体何を計算しているんだろう?
2008-10-10
